Algorithms (Deep Learning Ops)
Matrix Multiplication (Matmul)
\[C = A @ B\]The last dim of A and the first dim of B should match. For example, (2, 4) = (2, 3) @ (3, 4).
It works by taking a row of A and a column of B and performing two ops between them, multiplication and addition.
(2, 3)
A = [[0, 1, 2
3, 4, 5]]
(3, 4)
B = [[0, 1, 2, 3
4, 5, 6, 7
8, 9, 10, 11]]
(2, 4)
C = [[C(0), C(1), C(2), C(3)
C(4), C(5), C(6), C(7)]]
To compute the first element of C we have to multiple and add the first row of A and first column of B.
C(0) = A(0)*B(0) + A(1)*B(4) + A(2)*B(8)
C(0) = 0*0 + 1*4 + 2*8
C(0) = 20
and so on
CPU implementation
int rowsA = 2;
int colsB = 4;
int colsA = 3;
for (int rowA = 0; rowA < rowsA; rowA++) { // Iterate through rows of Matrix A or Matrix C
for (int colB = 0; colB < colsB; colB++) { // Iterate through columns of Matrix B or Matrix C
for (int sharedIndex = 0; sharedIndex < colsA; sharedIndex++) { // Iterate through the common dimension
// out[rowA][colB] += A[rowA][sharedIndex] * B[sharedIndex][colB]
out[rowA * colsB + colB] += A[rowA * colsA + sharedIndex] * B[sharedIndex * colsB + colB];
}
}
}
If you notice that the sharedIndex is the fastest moving index. To make things simpler, we can print out the indices
out[0] += A[0] * B[0]
out[0] += A[1] * B[4]
out[0] += A[2] * B[8]
--- innermost loop done (3 cols of A or 3 rows of B) ---
out[1] += A[0] * B[1]
out[1] += A[1] * B[5]
out[1] += A[2] * B[9]
--- innermost loop done (3 cols of A or 3 rows of B) ---
out[2] += A[0] * B[2]
out[2] += A[1] * B[6]
out[2] += A[2] * B[10]
--- innermost loop done (3 cols of A or 3 rows of B) ---
out[3] += A[0] * B[3]
out[3] += A[1] * B[7]
out[3] += A[2] * B[11]
and so on
To understand the way the indexing works, we need to lay out the matrix the way it is laid out in memory
(2, 3)
a = [(0, 0), (0, 1), (0, 2)
(1, 0), (1, 1), (1, 2)]
a = [0, 1, 2
3, 4, 5]
In memory, eveything is laid out as 1D.
[0, 1, 2, 3, 4, 5]
Now to access say (1, 2) element, the formula is
a(1, 2) = current_row * no_of_cols + current_column
This multiplication (current_row * no_of_cols) takes the pointer to
the starting index of a row, in this case 3.
Next the additon (+ current_column) offsets the pointer to the
column required, in this case 2. Therefore
a(1, 2) = (1*3) + 2
a(1, 2) = 5
Now the above implementation is not cache-friendly. In other words, it is not an efficient algorithm. It makes sense, since if we look at B matrix, for every iteration of the loop we are skipping colsB/sharedIndex length to retrive the next item. This is not good.
Whats good for the cache and speed is that we retrieve/store elements that are adjacent to one another.
If we go back to the way matmul is done and observe the successive iterations of the intermost loop
out[0] += A[0] * B[0]
--- innermost loop done (3 cols of A or 3 rows of B) ---
out[1] += A[0] * B[1]
--- innermost loop done (3 cols of A or 3 rows of B) ---
out[2] += A[0] * B[2]
--- innermost loop done (3 cols of A or 3 rows of B) ---
out[3] += A[0] * B[3]
and so on
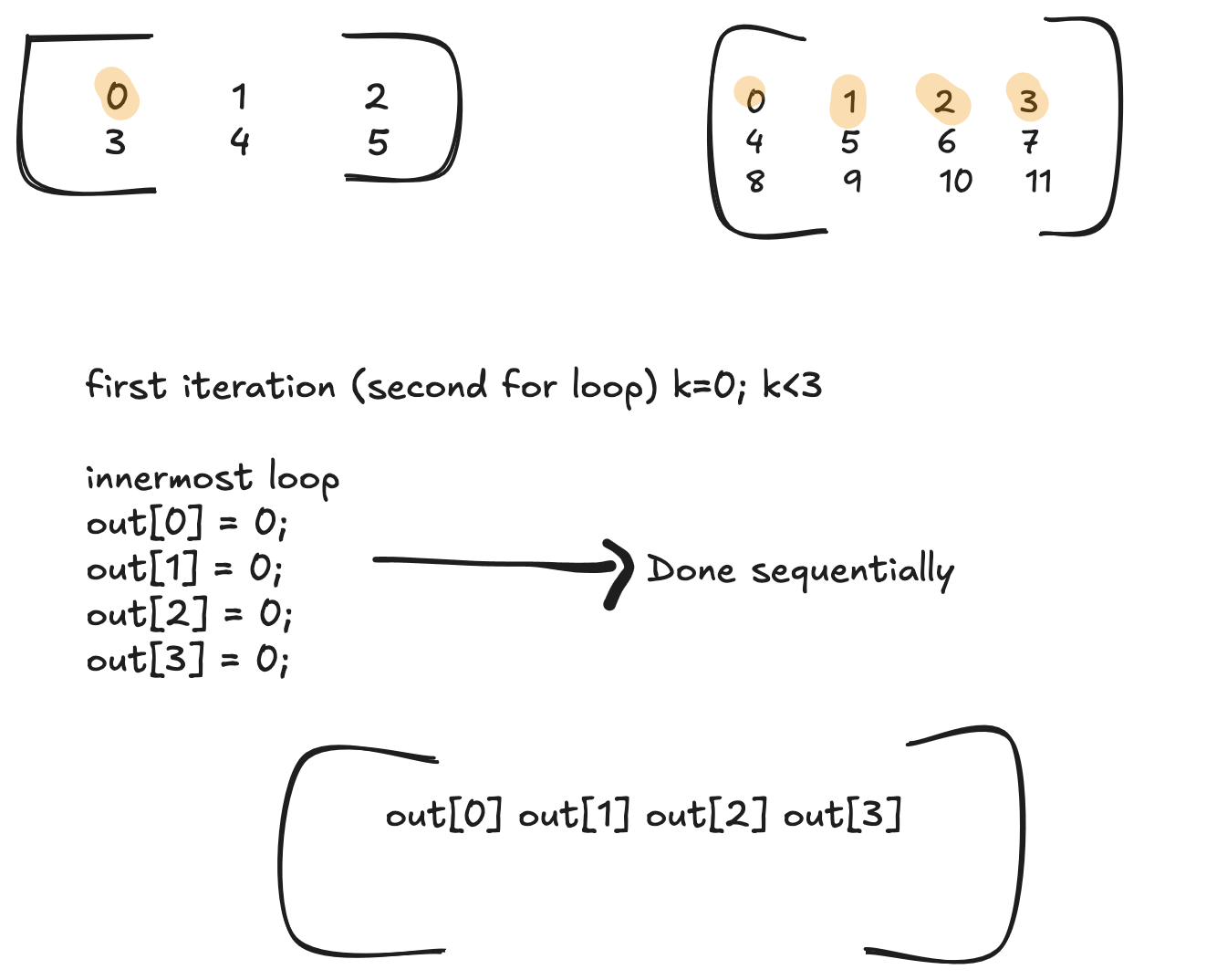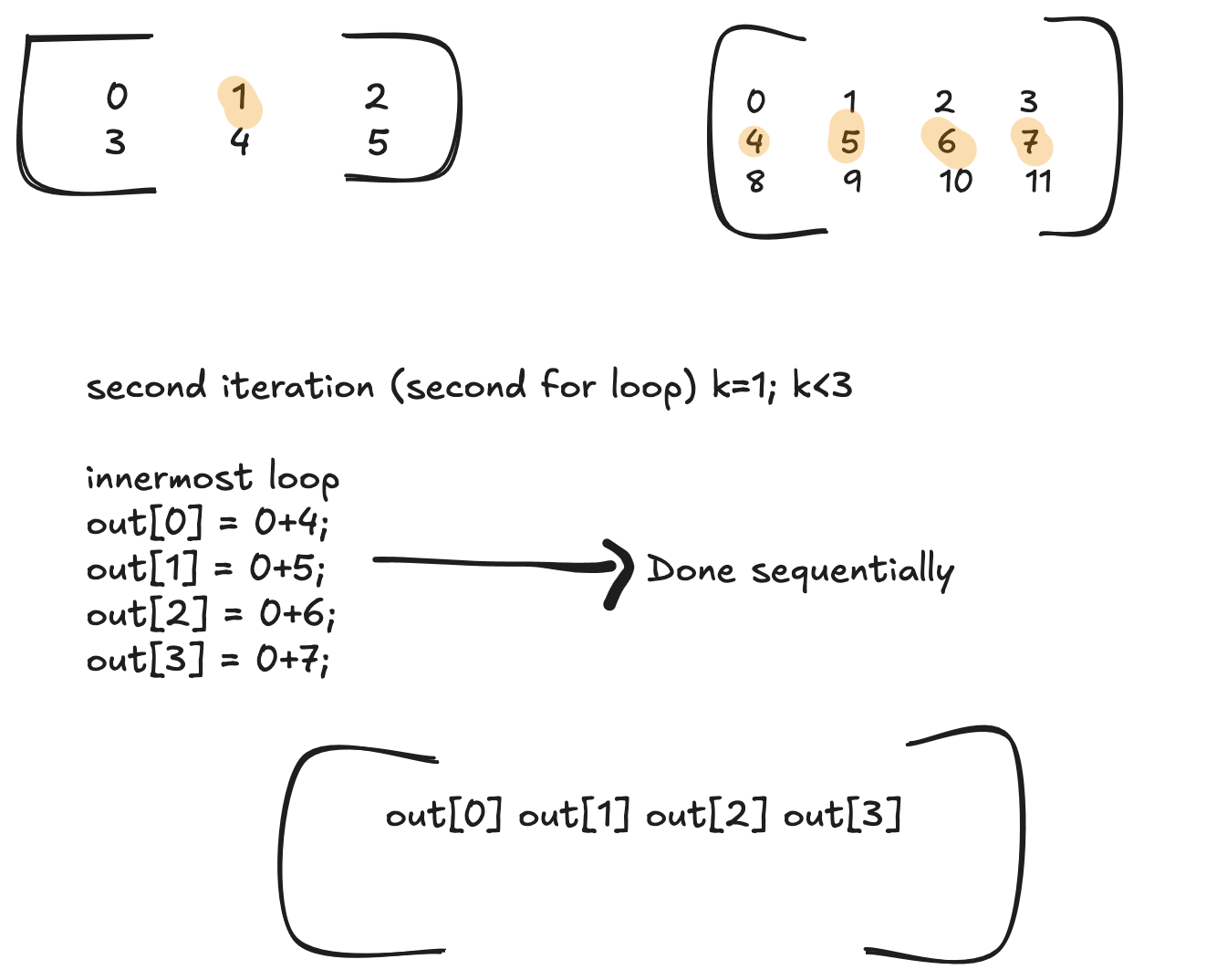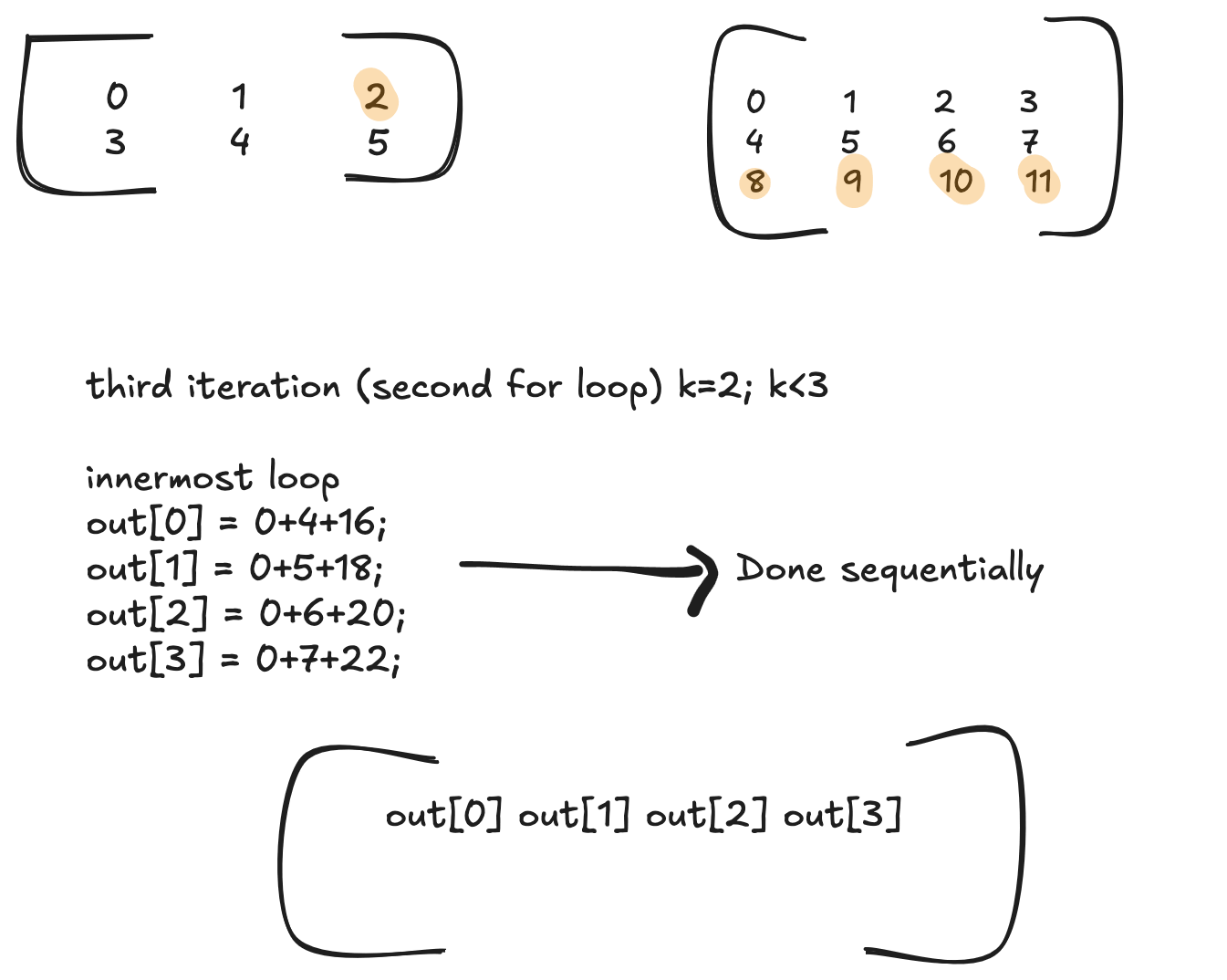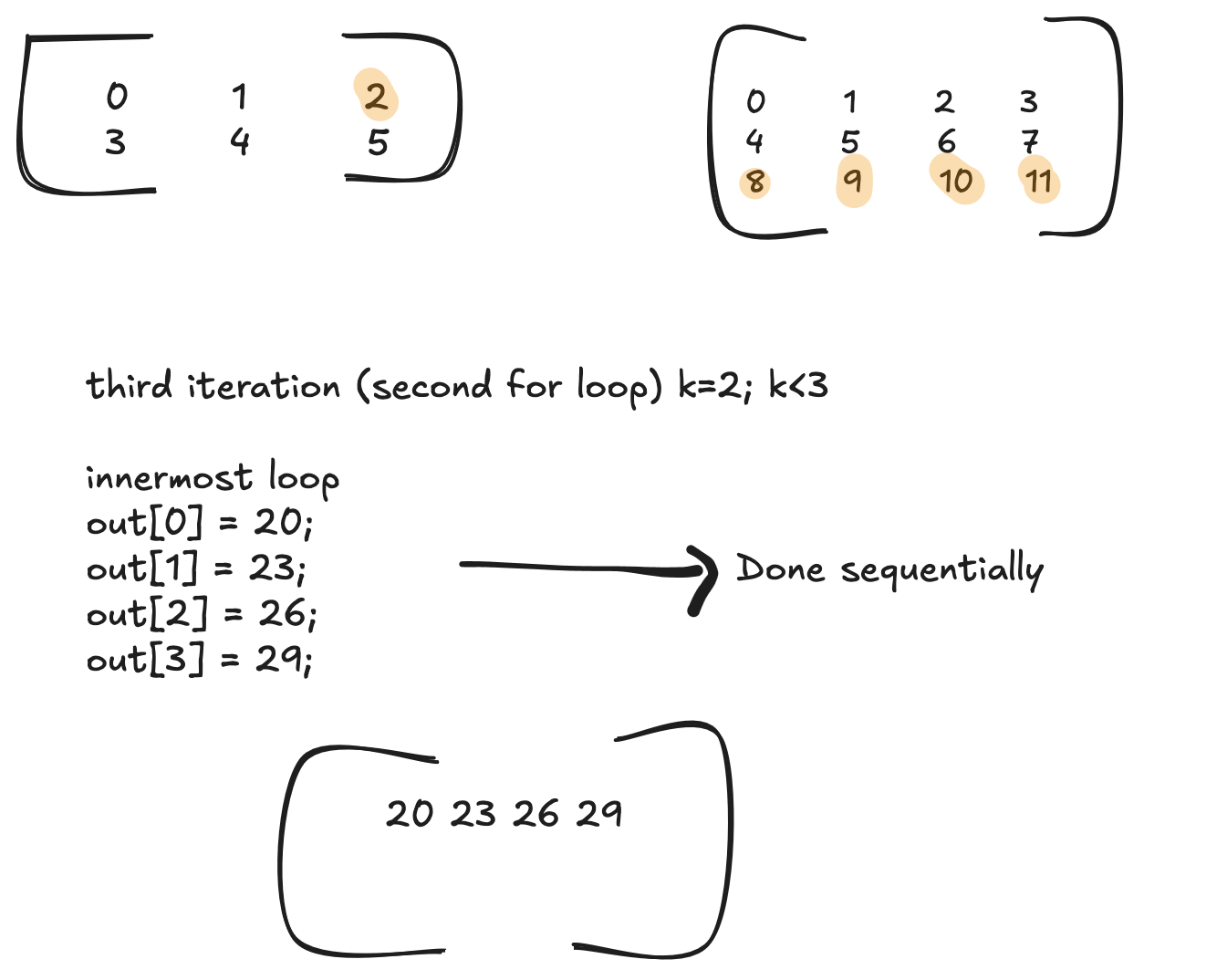
We can observe that for the for every element in a row of C, adjacent elements of A and B are used. Or in other words, for every row of C, if we loop through it colsB times and keep accumulating the respective element, we have essentially done matmul. We do not have to skip colsB time everytime.
In the C code, all we have to do to achieve this, is by interchanging the last and second last loop
int rowsA = 2;
int colsB = 4;
int colsA = 3;
for (int rowA = 0; rowA < rowsA; rowA++) { // Iterate through rows of A or C
for (int sharedIndex = 0; sharedIndex < colsA; sharedIndex++) { // Iterate through shared dimension
for (int colB = 0; colB < colsB; colB++) { // Iterate through columns of B or C
// out[rowA][colB] += A[rowA][sharedIndex] * B[sharedIndex][colB]
out[rowA * colsB + colB] += A[rowA * colsA + sharedIndex] * B[sharedIndex * colsB + colB];
}
}
}
The colB is the fastest moving index.
out[0] += A[0] * B[0]
out[1] += A[0] * B[1]
out[2] += A[0] * B[2]
out[3] += A[0] * B[3]
--- innermost loop done (4 cols of B) ---
out[0] += A[1] * B[4]
out[1] += A[1] * B[5]
out[2] += A[1] * B[6]
out[3] += A[1] * B[7]
--- innermost loop done (4 cols of B) ---
out[0] += A[2] * B[8]
out[1] += A[2] * B[9]
out[2] += A[2] * B[10]
out[3] += A[2] * B[11]
and so on
Here is a gif showing the cache efficient way of doing matmul (the iteration shown is the second loop and the innermoost loop are the multiplies and add)
GPU implementation
The same principles apply to the GPU as well, ie, things are more efficient and faster when we retrieve or store items in consecutive memory addresses, this is called memory coalescing in GPU jargon.
The way we achieve this is by using the naive algorithm. It makes sense when we shift our mind to the way GPU’s work.
Lets go back to the the naive implementation
out[0] += A[0] * B[0]
out[0] += A[1] * B[4]
out[0] += A[2] * B[8]
--- innermost loop done (3 cols of A or 3 rows of B) ---
out[1] += A[0] * B[1]
out[1] += A[1] * B[5]
out[1] += A[2] * B[9]
--- innermost loop done (3 cols of A or 3 rows of B) ---
out[2] += A[0] * B[2]
out[2] += A[1] * B[6]
out[2] += A[2] * B[10]
--- innermost loop done (3 cols of A or 3 rows of B) ---
out[3] += A[0] * B[3]
out[3] += A[1] * B[7]
out[3] += A[2] * B[11]
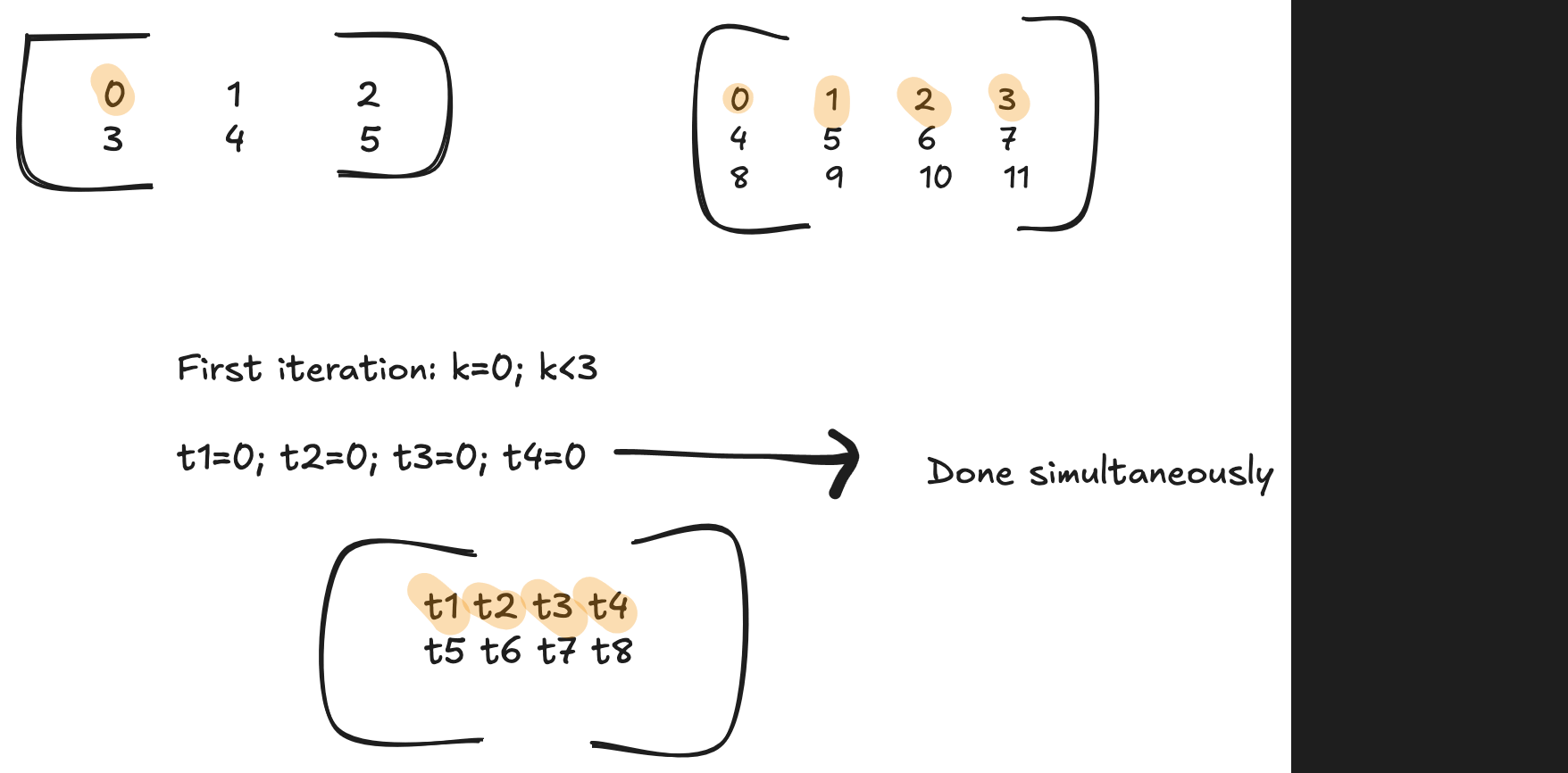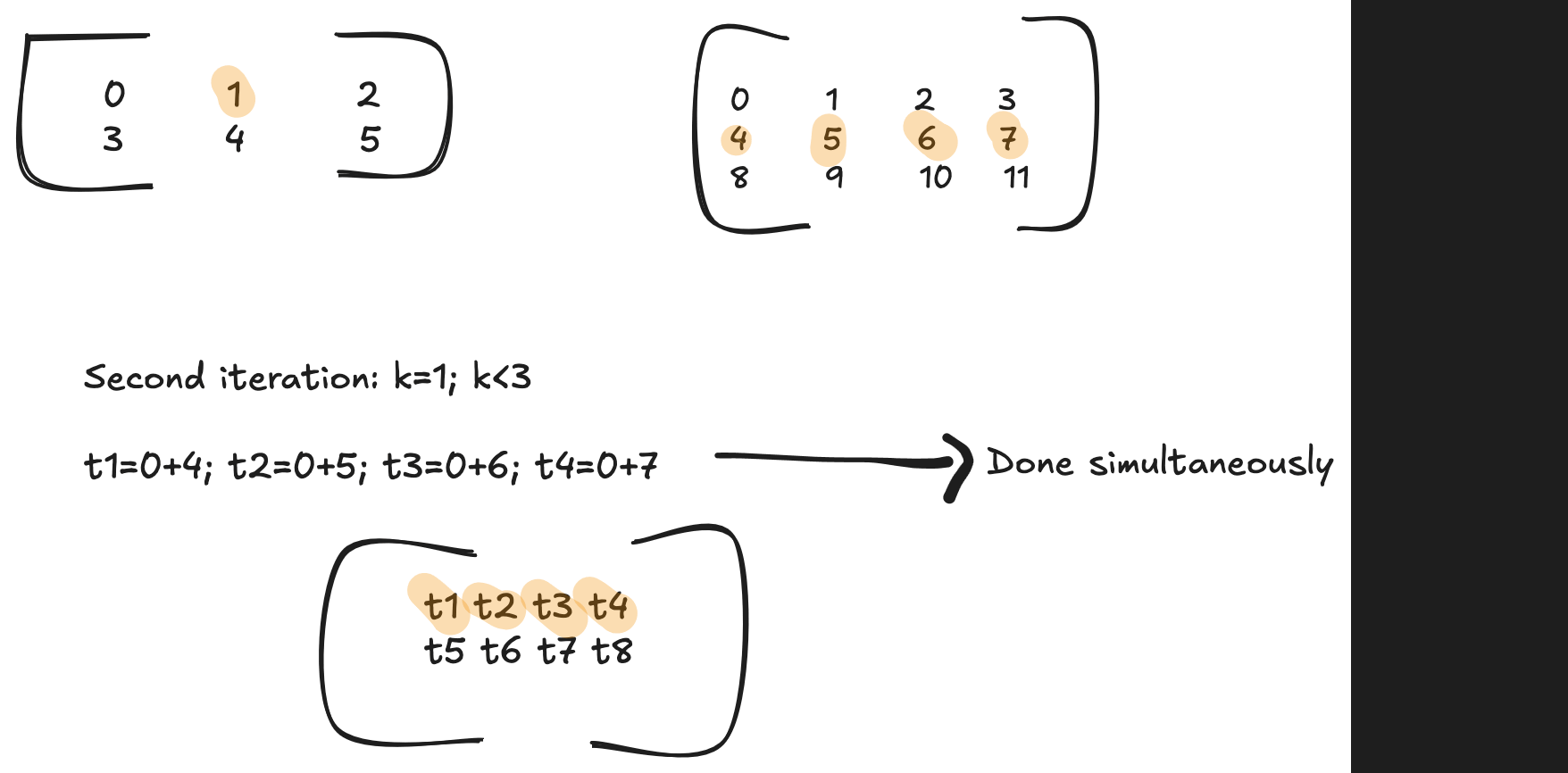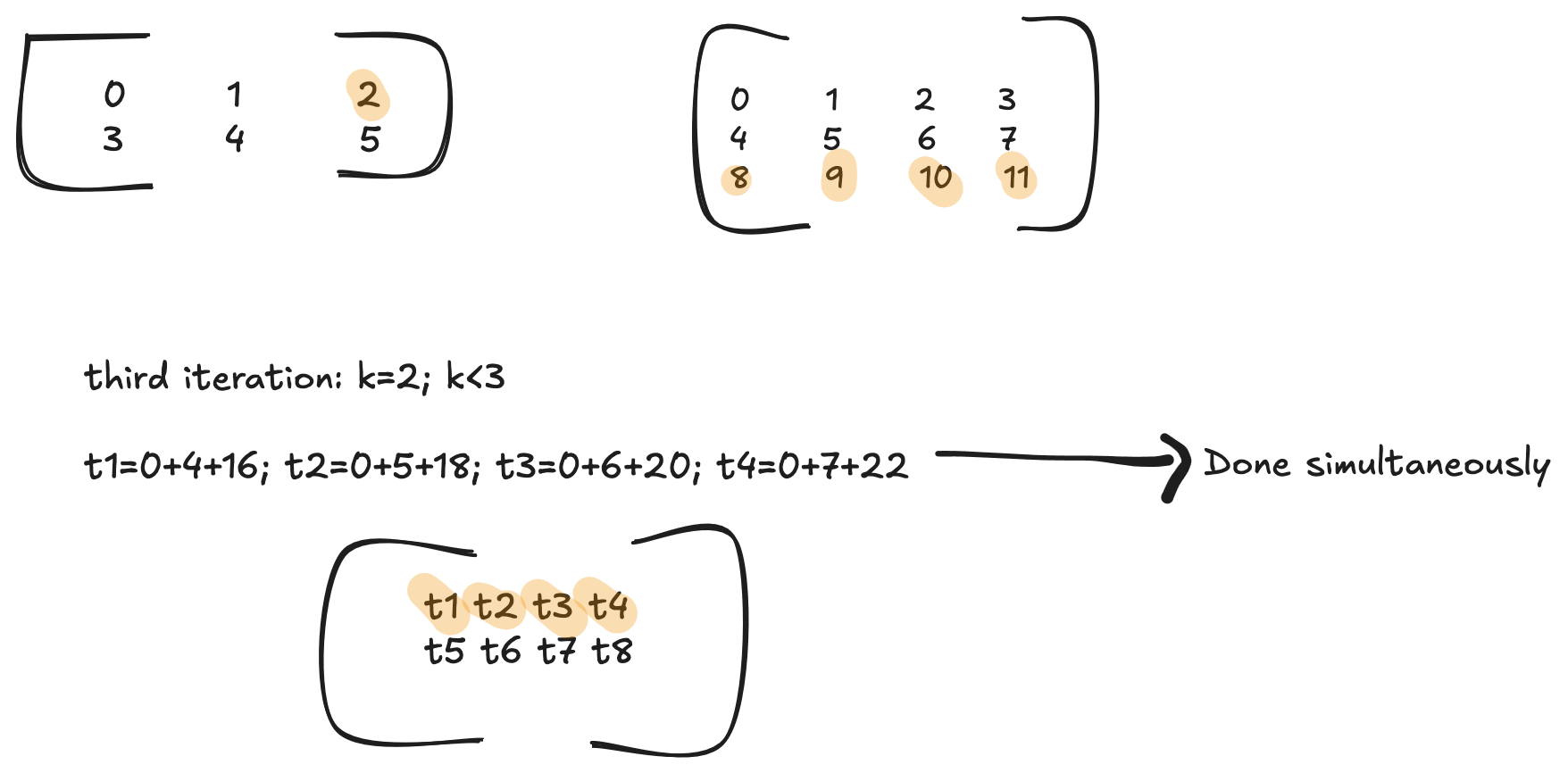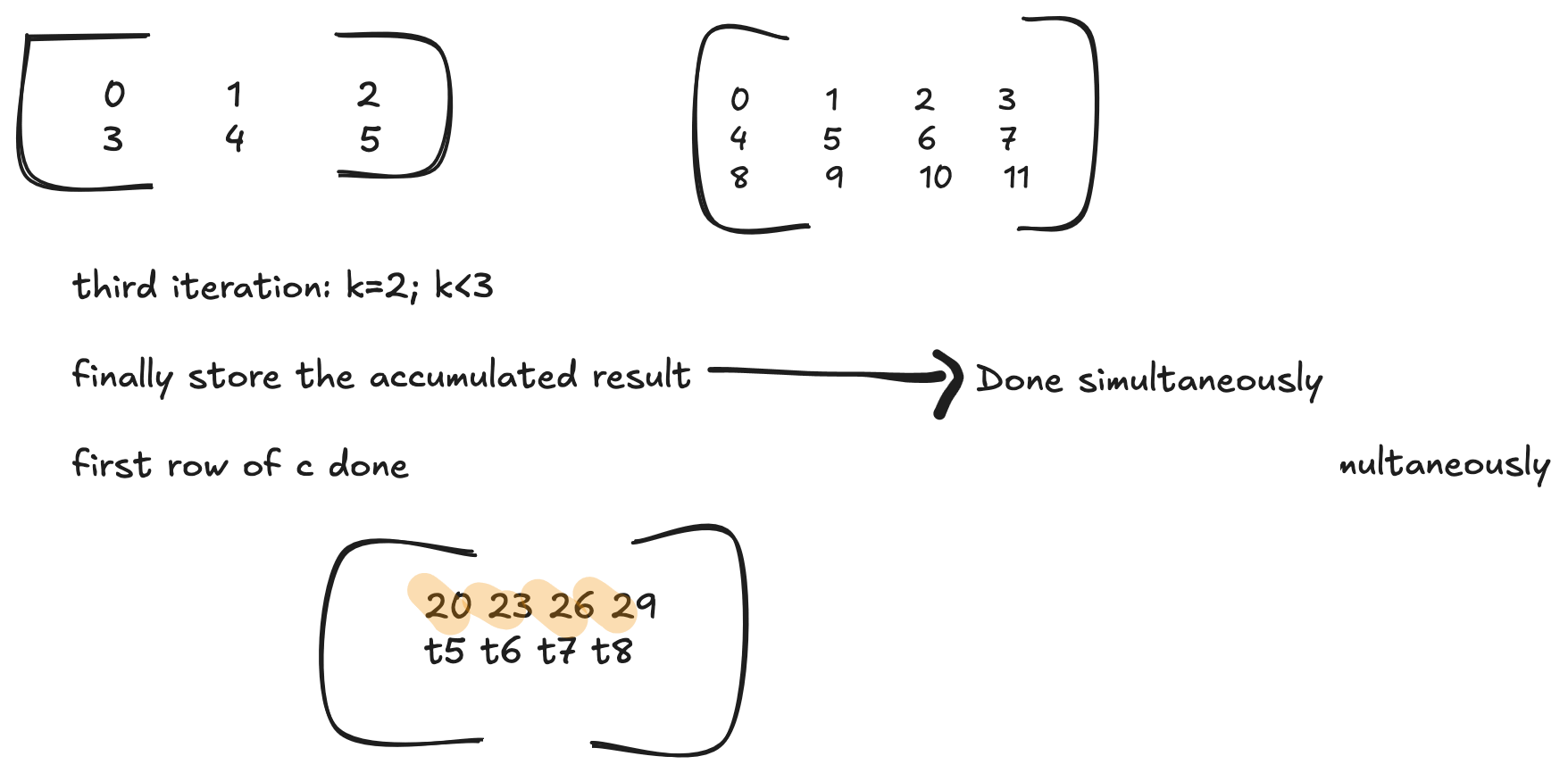
Please read my blog post on GPU Programming to understand the fundamentals. The first 2 for loops are launched as thread blocks. Now assuming the warp size is 4 (no of cols in C is 4), each thread in the first row (or in a warp) execute the same instruction. Which means iterating through the last for loop, all the 4 threads calculate the following simultaneously
// first iteration of the innermost loop, all of the below operation is done simultaneously
// 1st thread
out[0] += A[0] * B[0]
// 2nd thread
out[1] += A[0] * B[1]
// 3rd thread
out[2] += A[0] * B[2]
// 4th thread
out[3] += A[0] * B[3]
Each thread calculates its respective indices for A, B and C and all of them access memory that are adjacent to one other.